Some Basic Gray Level Transformations and Histogram Processing.

By -

1.Some Basic Gray Level Transformations

We begin the study of image enhancement techniques by discussing gray-level transformation functions.These are among the simplest of all image enhancement techniques.The values of pixels, before and after processing, will be denoted by r and s, respectively. As indicated in the previous section, these values are related by an expression of the form s=T(r), where T is a transformation that maps a pixel value r into a pixel value s. Since we are dealing with digital quantities, values of the transformation function typically are stored in a one-dimensional array and the mappings from r to s are implemented via table lookups. For an 8-bit environment, a lookup table containing the values of T will have 256 entries.

As an introduction to gray-level transformations, consider Fig. 3.3, which shows three basic types of functions used frequently for image enhancement: linear (negative and identity transformations), logarithmic (log and inverse-log transformations), and power-law (nth power and nth root transformations).The identity function is the trivial case in which output intensities are identical to input intensities. It is included in the graph only for completeness.

clip_image002

Image Negatives

The negative of an image with gray levels in the range [0,L-1]is obtained by using the negative transformation shown in Figure. 3.3, which is given by the expression

s = L - 1 - r.

image

Reversing the intensity levels of an image in this manner produces the equivalent of a photographic negative. This type of processing is particularly suited for enhancing white or gray detail embedded in dark regions of an image, especially when the black areas are dominant in size. An example is shown in . The original image is a digital mammogram showing a small lesion. In spite of the fact that the visual content is the same in both images, note how much easier it is to analyse the breast tissue in the negative image in this particular case.

Log Transformations

s = c log (1 + r)

where c is a constant, and it is assumed that r _ 0.The shape of the log curve in shows that this transformation maps a narrow range of low gray-level

values in the input image into a wider range of output levels.The opposite is true

of higher values of input levels.We would use a transformation of this type to expand the values of dark pixels in an image while compressing the higher-level

values.The opposite is true of the inverse log transformation.Any curve having the general shape of the log functions shown in Fig. would accomplish this spreading/compressing of gray levels in an image.

In fact,

image

the power-law transformations discussed in the next section are much more versatile for this purpose than the log transformation. However, the log function has the important characteristic that it compresses the dynamic range of images with large variations in pixel values.A classic illustration of an application in which pixel values have a large dynamic range is the Fourier spectrum, which will be discussed in Chapter 4. At the moment, we are concerned only with the image characteristics of spectra. It is not unusual to encounter spectrum values

In fact, the power-law transformations discussed in the next section are much more versatile for this purpose than the log transformation. However, the log function has the important characteristic that it compresses the dynamic range of images with large variations in pixel values.A classic illustration of an application

in which pixel values have a large dynamic range is the Fourier spectrum, which will be discussed in Chapter 4. At the moment, we are concerned only with the

image characteristics of spectra. It is not unusual to encounter spectrum values that range from 0 to or higher.While processing numbers such as these presents no problems for a computer, image display systems generally will not be able to reproduce faithfully such a wide range of intensity values. The net effectis that a significant degree of detail will be lost in the display of a typical Fourier spectrum.

2. Histogram Processing

image

The histogram of a digital image with gray levels in the range [0, L-1] is a discrete function hArkB=nk, where rk is the kth gray level and nk is the number

of pixels in the image having gray level rk. It is common practice to normalize a histogram by dividing each of its values by the total number of pixels in the image, denoted by n. Thus, a normalized histogram is given by pArkB=nk_n, for k=0, 1,p ,L-1. Loosely speaking, pArkB gives an estimate of the probability of occurrence of gray level rk. Note that the sum of all components of a normalized histogram is equal to 1.

Histograms are the basis for numerous spatial domain processing techniques. Histogram manipulation can be used effectively for image enhancement, as shown in this section. In addition to providing useful image statistics, we shall see in subsequent chapters that the information inherent in histograms also is quite useful in other image processing applications, such as image compression and segmentation. Histograms are simple to calculate in software and also lend themselves to economic hardware implementations, thus making them a popular tool for real-time image processing.

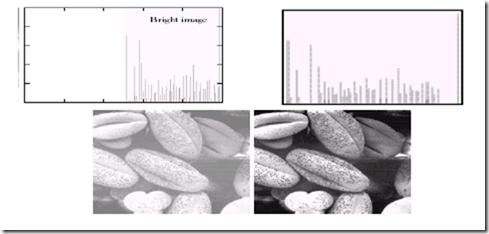
As an introduction to the role of histogram processing in image enhancement, consider which is the pollen image shown in four basic gray-level characteristics: dark, light, low contrast, and high contrast.The right side of the figure shows the histograms corresponding to these images. The horizontal axis of each histogram plot corresponds to gray level values, rk. The vertical axis corresponds to values of hArkB=nk or pArkB=nk_n if the values are normalized.Thus, as indicated previously, these histogram plots are simply plots of hArkB=nk versus rk or pArkB=nk_n versus rk.

Comments

Post a Comment

Popular posts from this blog

Top hat transformation

By -
Image
• The top hat transformation is used as a simple tool for segmenting objects in gray-scale images that differ in brightness from background, even when the background is of uneven gray-scale. • The top hat transform is superseded by the watershed segmentation for more complicated backgrounds. • Assume a gray-level image X and a structuring element K. The residue of opening as compared to original image X ∖ (X ∘ K) constitutes a new useful operation called a Top hat transformation. • The top hat transformation is a good tool for extracting light objects on a dark but slowly changing background. Those parts of the image that cannot fit into structuring element K are removed by opening. • Subtracting the opened image from the original provides an image where removed objects stand out. • The actual segmentation can be performed by simple thresholding (Fig 18). • If an image were a hat, the transformation would extract only the top of it, provided that the structuring element is larger...
Read more

Digital Image Processing part1

By -
Image
SEGMENTATION THRESHOLDING • Segmentation is the process of partitioning a digital image into multiple segments (sets of pixels, also known as super pixels). • The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze. • Image segmentation is typically used to locate objects and boundaries (lines, curves, etc.) in images. • More precisely, image segmentation is the process of assigning a label to every pixel in an image such that pixels with the same label share certain visual characteristics. • Complete segmentation - set of disjoint regions uniquely corresponding with objects in the input image. • Cooperation with higher processing levels which use specific knowledge of the problem domain is necessary. • Partial segmentation - regions do not correspond directly with image objects. • Image is divided into separate regions that are homogeneous with respect to a chosen property such as bright...
Read more

Basics of Spatial Filtering,Frequency Domain filters and Homomorphic filtering

By -
Image
Basics of Spatial Filtering some neighborhood operations work with the valuesof the image pixels in the neighborhood and the corresponding values of asubimage that has the same dimensions as the neighborhood.The subimage iscalled a f i l t e r , m ask , k ernel, template, or window , with the first three terms beingthe most prevalent terminology.The values in a filter subimage are referred toas coefficients , rather than pixels. The concept of filtering has its roots in the use of the Fourier transform for signal processing in the so-called f r equency domain . This topic is discussed in more detail in Chapter 4. In the present chapter, we are interested in filtering operations that are performed directly on the pixels of an image.We use the term spatial filtering to differentiate this type of process from the more traditional frequency domain filtering. The mechanics of spatial filtering are illustrated infig.The process consists simply of moving the filter mask from point to poi...
Read more