Digital Image Processing part1
SEGMENTATION
THRESHOLDING
• Segmentation is the process of partitioning a digital image into multiple segments (sets of pixels, also known as super pixels).
• The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze.
• Image segmentation is typically used to locate objects and boundaries (lines, curves, etc.) in images.
• More precisely, image segmentation is the process of assigning a label to every pixel in an image such that pixels with the same label share certain visual characteristics.
• Complete segmentation - set of disjoint regions uniquely corresponding with objects in the input image.
• Cooperation with higher processing levels which use specific knowledge of the problem domain is necessary.
• Partial segmentation - regions do not correspond directly with image objects.
• Image is divided into separate regions that are homogeneous with respect to a chosen property such as brightness, color, reflectivity, texture, etc.
• In a complex scene, a set of possibly overlapping homogeneous regions may result. The partially segmented image must then be subjected to further processing, and the final image segmentation may be found with the help of higher level information.
• Simple segmentation problems:
o contrasted objects on a uniform background
o Simple assembly tasks, blood cells, printed characters, etc.
• Totally correct and complete segmentation of complex scenes usually cannot be achieved in this processing phase.
• A reasonable aim is to use partial segmentation as an input to higher level processing.
• Segmentation problems:
o image data ambiguity
o information noise
• Segmentation methods
o global approaches, e.g. using histogram of image features
o edge-based segmentations
o region-based segmentations
• Characteristics used in edge detection or region growing are brightness, texture, velocity field, etc...
Thresholding
• The simplest method of image segmentation is called the thresholding method. This method is based on a clip-level (or a threshold value) to turn a gray-scale image into a binary image.
• The key of this method is to select the threshold value (or values when multiple-levels are selected). Several popular methods are used in industry including the maximum entropy method, Otsu's method (maximum variance), and k-means clustering.
[Threshold-> Strip of wood or stone forming the bottom of a doorway and crossed in entering a house or room.
A level or point at which something starts or ceases to happen or come into effect. The level at which one starts to feel or react to something.]
• The purpose of thresholding is to extract those pixels from some image which represent an object (either text or other line image data such as graphs, maps).
• Though the information is binary the pixels represent a range of intensities.
• Thus the objective of binarization is to mark pixels that belong to true foreground regions with a single intensity and background regions with different intensities.
• Thresholding is the transformation of an input image f to an output (segmented).
Binary image g as follows
• Where T is the thresholding, g(i,j)=1 for image elements of objects, and g(i,j)=0 for image elements of background
• If objects do not touch each other, and if their gray-levels are clearly distinct from background gray-levels, thresholding is suitable segmentation method.
• Correct threshold selection is crucial for successful threshold segmentation; this selection can be determined interactively or it can be the result of some threshold detection method.
• Only under very unusual circumstances can threshold be successful using a single threshold for whole image(global thresholding) since even in very simple images there are likely to be gray-level variations in objects and background; this variation may be due to non-uniform lighting, non- uniform input device parameters or a number of other factors.
• Segmentation using variable thresholds (adaptive thresholding), in which the threshold value varies over the image as a function of local image characteristics.
• A global threshold is determined from the whole image f :
T=T (f) .
• Local Thresholds are position dependent
• Where is that image part in which the threshold is determined. One option is to divide the image f into sub images and determine a threshold independently in each subimages, it can be interpolated from thresholds determined in neighboring sub images. Each sub images is then processed with respect to its local threshold.
• Basic thresholding as defined has many modifications. One possibility is to segment an image into regions of pixels with gray-levels from a set D and into background otherwise (band thresholding):
• This thresholding can be useful, for instance, in microscopic blood cell segmentations, where a particular gray-level interval represents Cytoplasma, the background is lighter, and the cell kernel darker.
• This thresholding definition can serve as a border detector as well; assuming dark objects on a light background, some gray-levels between those of objects and background can be found only in the object borders.
Thresholding algorithms
• For a thresholding algorithm to be really effective, it should preserve logical and semantic content. There are two types of thresholding algorithms
o Global thresholding algorithms
o Local or adaptive thresholding algorithms
• In global thresholding, a single threshold for all the image pixels is used.
• When the pixel values of the components and that of background are fairly consistent in their respective values over the entire image, global thresholding could be used.
• In adaptive thresholding, different threshold values for different local areas are used.
Basic Global Thresholding
• Simplest of all thresholding techniques is to partition the image histogram by using a single global threshold, T.
• Segmentation is then accomplished by scanning the image pixel by pixel and labeling each pixel as object or background, depending on whether the gray level of that pixel is greater or less then the value of T.

• Fig 1(a) shows a simple image and Fig 1(b) shows its histogram, Fig1(c) shows the result of segmentation Fig 1 by using a threshold T midway between the maximum and minimum gray levels.
• This Threshold achieved a clean segmentation by eliminating the shadows and leaving only the objects themselves. The objects of interest in this case are darker than the background, so any pixel with a gray level<=T was labeled black (0) and any pixel with gray level>T was labeled white (255).
• The key objective is merely to generate a binary image, so the black-white relationship could be reversed.
Algorithm: Basic Global Thresholding
The following algorithm has been used to obtain the initial threshold T, in the following section automatically:
1. Choose initial estimate for T.
2. Divide the histogram using T. This will produce 2 groups of pixels:
• G1 - Set of all pixels with grey level values >T.
• G2 - Set of pixels with values <=T.
3. Compute the average grey level values m1 and m2 for the pixels in regions G1 and G2.
4. Compute a new threshold value:
T=1/2(m1+m2)
Repeat steps 2 through 4 until the difference in T in successive iterations is smaller than a predefined parameter T0.
Basic Adaptive Thresholding:
• Single value thresholding will not work to divide an image into sub images and threshold these individually.
• An approach for handling such a situation is to divide the original image into sub images and then utilize a different threshold to segment each sub image.
• The key issues in this approach are how to subdivide the image and how to estimate the threshold for each resulting sub image. Since the threshold used for each pixel depends on the location of the pixel in terms of the sub images, this type of thresholding is adaptive.
Fig 2: (a) Original Image (b) Result of global thresholding (c)Image subdivided into individual sub images (d)Result of adaptive thresholding
• Fig 2(a) which we concluded could not be thresholded effectively with a single global threshold previously.
• Fig 2(b) shows the result of thresholding the image with a global threshold manually placed in the valley of its histogram.
• One approach to reduce the effect of non uniform illumination is to subdivide the image into smaller sub images, such that the illumination of each sub image is approximately uniform.
• Fig 2(c) shows such a partition, obtained by subdividing the image into four equal parts, and then subdividing each part by four again.
• All the sub images that did not contain a boundary between object and background had variances of less than 75; All sub images containing boundaries had variances in excess of 100.
• Each sub image with variance greater than 100 was segmented with a threshold computed for that sub image using the algorithm.
• The initial value for T in each case was selected as the point midway between the minimum and maximum gray levels in the sub image.
• All sub images with variance less than 100 were treated as one composite image, which was segmented using a single threshold estimated using the same algorithm.
• The result of segmentation using this procedure is shown in Fig 2(d).
Threshold Detection Methods P-Tile (Percentile) Thresholding:
• This Technique uses knowledge about the area size of the desired object to the threshold an image.
• If some property of an image after segmentation is known a priori, the task of threshold selection is simplified, since the threshold is chosen to ensure that this property is satisfied.
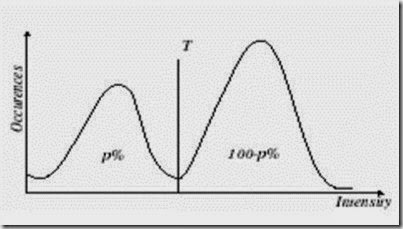
• A printed text sheet may be an example if we know that character of the text cover 1/p of the sheet area. Using this prior information about the ratio between the sheet area and character area, it is very easy to choose a threshold T (based on the image histogram) such that 1/p of the image area has gray values less than T and the rest has gray values larger than T. This method is called P-tile thresholding.
• P-tile Method:- If object occupies P% of image pixels the set a threshold T such that P% of pixels have intensity below T.
Histogram Shape Analysis:-
• If the image consists of objects of approximately the same gray-level that differs from the gray-level of the background, the resulting histogram is bi- modal.
• Pixels of objects form one of its peaks, while pixels of the background form the second peak.
• The histogram shape illustrates the fact that the gray values between the two peaks are not common in the image, and probably result from border pixels between objects and background.
• The chosen threshold must meet minimum segmentation error requirements; it makes intuitive sense to determine the threshold as the gray-level that has a minimum histogram value between the two mentioned maxima.
• If the histogram is multi-modal, more thresholds may be determined at minima between any two maxima. Each threshold gives different segmentation results.
Mode Method:-
• To decide if the histogram is bi-modal or multi-modal may not be so simple in reality, it often being impossible to interpret the significance of local histogram maxima.
• Bi-modal histogram threshold detection algorithms usually find the highest local maxima first and detect the threshold as a minimum between them; this technique is called the mode method.
• To avoid detection of two local maxima belonging to the same global maximum, a minimum distance in gray-levels between these maxima is usually required, or techniques to smooth histograms are applied.
• Assume that gray values are drawn from two normal distributions with parameters
• If the standard deviations are zero, there will be two spikes in the histogram and the threshold can be placed anywhere between them.
• For non-ideal cases, there will be peaks and valleys and the threshold can be placed corresponding to the valley
Optimal Thresholding:-
• Methods based on approximation of the histogram of an image using a weighted sum of two or more probability densities with normal distribution represent a different approach called optimal thresholding.
• The threshold is set as the closest gray-level corresponding to the minimum probability between the maxima of two or more normal distributions, which results in minimum error segmentation (the smallest number of pixels is mis-sementated).
• See Fig 3 the difficulty with these methods is in estimating normal distribution parameters together with the uncertainty is sought that maximizes gray-level variance between objects and background.
• Note that this approach can be applied even if more than one threshold is needed.
• Alternatively, minimization of variance of the histogram, sum of square errors, spatial entropy, average clustering, or other optimization approaches may be used.
Fig 3: Gray-level histograms approximated by two normal distributions—the threshold is set to give minimum probability of segmentation error. (a)Probability distributions of background and objects . (b)Corresponding histograms and optimal threshold
• The following algorithm represents a simpler version that shows a rationale for this approach and works well even if the image histogram is not bi- modal.
• This method assumes that regions of two main gray-levels are present in the image, thresholding of printed text being an example. The algorithm is iterative, four to ten iterations usually being sufficient.
Algorithm Iterative (optimal) Threshold selection:-
1. Assume no knowledge about the exact location of objects, consider as a first approximation that the four corners of the image contain background pixels only and the remainder contains object pixels.
2. At step t, compute and
as the mean background and object gray level, respectively, where segmentation into background and objects at step t is defined by the threshold value determined in the previous step
Segmentation: Edge-based segmentation
Edge-based Segmentation
• An edge is the boundary between an object and the background.
• Edge-based segmentation represents a large group of methods based on information about edges in the image
• Edge-based segmentations rely on edges found in an image by edge detecting operators
-- these edges mark image locations of discontinuities in gray level, color, texture, etc.
• Image resulting from edge detection cannot be used as a segmentation result.
• Supplementary processing steps must follow to combine edges into edge chains that correspond better with borders in the image.
• The final aim is to reach at least a partial segmentation -- that is, to group local edges into an image where only edge chains with a correspondence to existing objects or image parts are present.
• The more prior information that is available to the segmentation process, the better the segmentation results that can be obtained.
• The most common problems of edge-based segmentation are
o an edge presence in locations where there is no border, and
o no edge presence where a real border exists.
Edge image thresholding
• Almost no zero-value pixels are present in an edge image, but small edge values correspond to non-significant gray level changes resulting from quantization noise, small lighting irregularities, etc. Simple Thresholding of an edge image can be applied to remove these small values. The approach is based on an image of edge magnitudes processed by an appropriate threshold.
• Selection of an appropriate global threshold is often difficult and sometimes impossible; p-tile thresholding can be applied to define a threshold
• Alternatively, non-maximal suppression and hysteresis thresholding can be used as was introduced in the Canny edge detector.
Fig 1: Edge image thresholding (a)Original image (b)Edge image (c)Edge image thresholding at 30 (d)Edge image thresholding at 10
Algorithm : Non Maximal suppression of directional edge data
1. Quantize edge directions eight ways according to 8-connectivity
2. For each pixel with non-zero edge magnitude, inspect the two adjacent pixels indicated by the direction of its edge
3. If the edge magnitude of either of these two exceeds that of the pixel under inspection, mark it for deletion.
4. When all pixels have been inspected, re-scan the image and erase to zero all edge data marked for deletion.
This algorithm is based on 8-connectivity and may be simplified for 4-coonectivity; it is also open to more sophisticated measurement of edge direction.
Algorithm: Hysteresis output of an edge detector
1. Mark all edges with magnitude greater than as correct.
2. Scan all pixels with edge magnitude in the range [,
].
3. If such a pixel borders another already marked as an edge, then mark it too. ‘Bordering’ may be defined by 4- or 8- connectivity.
4. Repeat from step 2 until stability.
Fig 2 (a)Non-maximal suppression of the data (b)Hysteresis applied to (a).
Edge relaxation
• Borders resulting from the previous method are strongly affected by image noise, often with important parts missing.
• Considering edge properties in the context of their mutual neighbors can increase the quality of the resulting image.
• All the image properties, including those of further edge existence, are iteratively evaluated with more precision until the edge context is totally clear - based on the strength of edges in a specified local neighborhood, the confidence of each edge is either increased or decreased.
• A weak edge positioned between two strong edges provides an example of context; it is highly probable that this inter-positioned weak edge should be a part of a resulting boundary.
• If, on the other hand, an edge (even a strong one) is positioned by itself with no supporting context, it is probably not a part of any border.
• Edge context is considered at both ends of an edge, giving the minimal edge neighborhood.
• The central edge e has a vertex at each of its ends and three possible border continuations can be found from both of these vertices.
• Vertex type -- number of edges emanating from the vertex, not counting the edge e.
• The type of edge e can then be represented using a number pair i-j describing edge patterns at each vertex, where i and j are the vertex types of the edge e.
Fig 4 Edge patterns and corresponding edge types
1-1 isolated edge- negative influence on the edge confidence,
1-2 uncertain- weak positive, or no influence on edge confidence,
1-3,0-3 dead end- negati9ve influence on edge confidence,
1-1 continuation- strong positive influence on edge confidence,
1-2,1-3 continuation to border intersection- medium positive influence on edge confidence,
2-2,2-3,3-3 bridge between borders- not necessary for segmentation, no influence on edge confidence.
• Edge relaxation is an iterative method, with edge confidences converging either to zero (edge termination) or one (the edge forms a border).
• The confidence of each edge e in the first iteration can be defined as a normalized magnitude of the crack edge,
o with normalization based on either the global maximum of crack edges in the whole image, or on a local maximum in some large neighborhood of the edge
Algorithm: Edge Relaxation
1.Evaluate a confidence (e) for all crack edges e in the image.
2. Find the edge type of each edge based on edge confidences (e) in its neighborhood.
3. Update the confidence (e) of each edge e according to its type and its previous confidence
(e).
4. Stop if all edge confidences have converged either to 0 or 1. Repeat steps 2 and 3 otherwise.
Fig 5 Edge relaxation (a) Resulting borders after 10 iterations (b) Borders after thinning.
Fig 5 (c) Borders after 100 iterations, thinned (d) Borders after 100 iterations overlaid over original.
• The main steps of the above Algorithm are evaluation of vertex types followed by evaluation of edge types, and the manner in which the edge confidences are modified.
• A vertex is considered to be of type i if
• where a,b,c are the normalized values of the other incident crack edges
• m=max (a,b,c,q) ... the introduction of the quantity q ensures that type (0) is non-zero for small values of a.
• For example, choosing q=0.1, a vertex (a,b,c) = (0.5, 0.05, 0.05) is a type 1 vertex, while a vertex (0.3, 0.2, 0.2) is a type 3 vertex.
• Similar results can be obtained by simply counting the number of edges emanating from the vertex above a threshold value.
• Edge type is found as a simple concatenation of vertex types, and edge confidences are modified as follows:
• Edge relaxation, as described above, rapidly improves the initial edge labeling in the first few iterations.
• Unfortunately, it often slowly drifts giving worse results than expected after larger numbers of iterations.
• The reason for this strange behavior is in searching for the global maximum of the edge consistency criterion over all the image, which may not give locally optimal results.
• A solution is found in setting edge confidences to zero under a certain threshold, and to one over another threshold which increases the influence of original image data.
• Where and
are parameters controlling the edge relaxation convergence speed and resulting border accuracy.
• This method makes multiple labeling possible; the existence of two edges at different directions in one pixel may occur in corners, crosses, etc.
• The relaxation method can easily be implemented in parallel.
Border tracing
• If a region border is not known but regions have been defined in the image, borders can be uniquely detected.
• First, let us assume that the image with regions is either binary or that regions have been labeled.
• An inner region border is a subset of the region
• An outer border is not a subset of the region.
• The following algorithm covers inner boundary tracing in both 4-connectivity and 8- connectivity.

















Comments
Post a Comment