Hit-or-miss transformation

• Hit-or-miss transformation is the morphological operator for finding local patterns of pixels, where local means the size of the structuring element.

• It is a variant of template matching that finds collections of pixels with certain shape properties.

• Structuring element B, Tested points X, operation denoted by a pair of disjoint sets B = (Bl, B2), called a composite structuring element.

• The Hit-or-miss transformation ⊗ is defined as

• Finding local patterns in image Bl tests objects, B2 background (complement), Useful for finding corners, for instance.

• The hit-or-miss transformation operates as a binary matching between an image X and the structuring element(Bl, B2). It may be expressed using

erosions and dilations as well

Opening and closing

• Erosion and dilation are not inverse transformation—if an image is eroded and then dilated, the original image is not re-obtained.

• Erosion followed by dilation is called opening. The opening of an image X by the structuring element B is denoted by X ∘ B and is defined as

X ∘ B = (X ⊖ B) ⊕ B.

• Dilation followed by erosion is called Closing. The closing of an image X by the structuring element B is denoted by X ∙ B and is defined as

X ∙ B = (X ⊕ B) ⊖ B.

• If an image X is unchanged by opening with the structuring element B , it is called open with respect to B . Similarly , if an image X is unchanged by closing with B , it is called as closed with respect to B.

• Opening and closing with an isotropic structuring element is used to eliminate specific image details smaller than the structuring element—the global shape of the objects is not distorted.

• Closing connects objects that are close to each other, fills up small holes, and smoothes the object outline by filling up narrow gulfs.

Fig 9: Opening (original on left)

Fig 10: Closing (original on left)

• Opening and closing are invariant to translation of the structuring element.

• Opening is anti-extensive (X ∘ B ⊆ X) and closing is extensive (X ⊆ X ∙ B).

• Opening and closing are dual transformations

• Iteratively used opening and closings are idempotent, meaning that reapplication of these transformations does not change the previous result.

Gray scale dilation and erosion

• Binary morphological operations are extendible to gray-scale images using the ‘min’ and ‘max’ operations.

• Erosion – assigns to each pixel minimum value in a neighborhood of corresponding pixel in input image

° structuring element is richer than in binary case

° structuring element is a function of two variables, specifies desired local gray-level property

° Value of structuring element is subtracted when minimum is calculated in the neighborhood.

• Dilation – assigns maximum value in neighborhood of corresponding pixel in input image

° value of structuring element is added when maximum is calculated in the neighborhood

• Such extension permits topographic view of gray scale images

° Gray-level is interpreted as height of a particular location of a hypothetical landscape

° Light and dark spots in the image correspond to hills and valleys

° Such morphological approach permits the location of global properties of the images as valleys, mountain ridges (crests), watersheds.

Top surface, Umbra, and gray-scale dilation and erosion

• Consider a point set A in n -dimensional Euclidean space, A ⊂ ℇn

• Assume first (n − 1) co-ordinates of the set constitute a spatial domain and the nth co-ordinate corresponds to the value of a function or functions

at a point.

• The top surface of a set A is a function defined on the (n − 1) dimensional support.

• For each (n − 1) tuple, the top surface is the highest value of the last co- ordinate of A (Fig 11).

Fig 11: Top surface of the set A corresponds to maximal values of the function f(Xl, X2)

• Umbra of a function f defined on some subset F (support) of (n − 1) dimensional space.

• Umbra is a region of complete shadow resulting from obstructing the light by a non-transparent object.

• In mathematical morphology, the umbra of f is a set that consists of the  topsurfaceoffandeverythingbelowit(Fig12).

Fig 12: Umbra of the top surface of a set is the whole subspace below it.

• Umbra of an umbra of f is an umbra.

• Top surface and umbra in the case of a simple 1D gray scale image (Fig 13)

Fig 13: Example of a 1D function (left) and its umbra (right).

• The gray-scale dilation of two functions as the top surface of the dilation of their umbra’s can be defined.

° ⊕ on the left-hand side is dilation in the gray-scale image,

° ⊕ on the left-hand side is dilation of binary image.

• No new symbol is introduced here, same applies to erosion ⊖ also.

• For binary dilation, one function, say f represents an image and the second, k small structuring element. Fig 14 shows the function k that will play the role of structuring element.

• Fig 15 shows the dilation of the umbra of f by the umbra of k .

Fig 14: A structuring element: 1D function (left) and its umbra (right).

Fig 15: 1D example of gray-scale dilation. The umbra’s of the 1D function f and structuring element k are dilated first, U[f] ⊕ U[k] . The top surface of this dilated set gives the result, f⊕k=T{U[f] ⊕ U[k]}.

• A computationally plausible way to calculate dilation can be obtained by taking the maximum of set of sums:

(f ⊕ k)(X) = max{f(X − z) + k(z), z ∈ K, X − z ∈ F}.

• The computational complexity is the same as for convolution in linear filtering, where a summation of products is performed.

• The definition of gray-scale erosion is analogous to gray-scale dilation. The gray-scale erosion of two functions(point sets)

° Takes their umbras.

° Erodes them using binary erosion.

° Gives the result as the top surface.

Fig 16:1D example of gray-scale erosion: The umbras of 1D function f and the structuring element k are eroded first, [f] ⊖ U[k] . The top surface of this eroded set gives the result, f ⊖ k = T{U[f] ⊖ U[k]}.

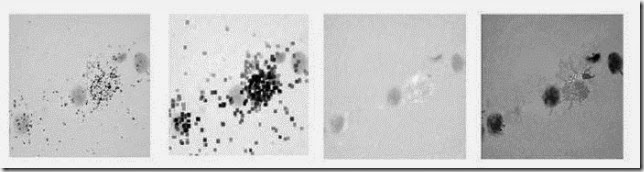
Example (Fig 17)

• This figure illustrates morphological pre-processing on a microscopic image of cells corrupted by noise.

• The aim is to reduce noise and locate individual cells.

• A 3x3 structuring element was used in erosion and dilation.

• The individual cells can be located by the reconstruction operation .The original image is used as a mask and the dilated image is an input for reconstruction.

Fig 17: Morphological pre-processing: (a)cells in a microscopic image corrupted by notes;(b)Eroded image;(c)Dilation of original image;(d)Reconstructed cells.

Umbra homeomorphism theorem, properties of erosion and dilation, opening and closing.

• The Umbra homeomorphism theorem states that the umbra operation is a homeomorphism from gray-scale morphology to binary morphology.

• The umbra homeomorphism is used for deriving properties of gray-scale operations.

• Gray-scale opening is defined as f ∘ k = (f ⊖ k) ⊕ k.

• Gray-scale closing is defined as f ∙ k = (f ⊕ k) ⊖ k.

• The duality between opening and closing is expressed as

−( f ∘ k)(X) = ((−f) ∙ k"" ) (X).

• The opening of f by structuring element k can be interpreted as sliding k on the landscape f. The position of all highest points reached by some part of k during the slide gives the opening, similar interpretation exists for erosion

Gray-scale opening and closing often used to extract parts of a gray-scale image with given shape and gray-scale structure.