Algorithm: Quad tree region identification

By -

1. First pass: search quad tree nodes in a given order –e.g., beginning from the root and in the NW, NE, SW, SE directions. Whenever an unlabeled non- zero leaf node is entered, a new label is assigned to it. Then search for neighboring leaf nodes in the E and S directions. If those leaves are non- zero and have not yet been labeled, assign the label of the node from which the search started. If the neighboring leaf node has already been labeled, store the collision information in an equivalence table.

2. Repeat step 1 until the whole tree has been searched.

3. Second pass: Re-label the leaf nodes of the quad tree according to the equivalence table.

Contour-based shape representation and description

• Region borders must be expressed in some mathematical form.

° Polar co-ordinates, in which border elements are represented as pairs of angle ö and distance r;

° Tangential co-ordinates, which codes the tangential directions 8(xn) of curve points as a function of path length n.

clip_image001

Fig 5: Co-ordinate systems. (a) Rectangular (Cartesian). (b)Polar (c) Tangential

Chain codes

• Chain codes describe an object by a sequence of unit-size line segments with a given orientation.

• The first element of such a sequence must bear information about its position to permit the region to be reconstructed. The process results in a sequence of numbers (Fig 6).

clip_image002

Fig 6: Chain code in 4-connectivity, and its derivative. Code: 3,0,0,3,0,1,1,2,1,2,3,2; derivative: 1,0,3,1,1,0,1,3,1,1,3,1.

• If the chain code is used for matching it must be independent of the choice of the first border pixel in the sequence.

• One possibility for normalizing the chain code is to find the pixel in the border sequence which results in the minimum integer number if the description chain is interpreted as a base four number -- that pixel is then used as the starting pixel.

° A mod 4 or mod 8 differences is called a chain code derivative, is another numbered sequence that represents relative directions of region boundary elements, measured as multiples of counter-

clockwise 900 or 450 direction changes (Fig 6).

Simple geometric border representation

• The following descriptors are mostly based on geometric properties of described regions. Because of the discrete character of digital images, all of them are sensitive to image resolution.

o Boundary length

Boundary length is derived from chain code representation. Vertical and horizontal steps have unit length of diagonal steps in 8- connectivity is ...2. A closed boundary length is evaluated from run length or quad tree representations. Boundary length increases as the image raster resolution increases.

o Curvature

Curvature is defined as the rate of change of slope. Values of the curvature at all boundary pixels can be represented by a histogram; relative numbers then provide information on how common specific boundary direction changes are. Histogram of boundary angles, such as the f3 angle in Fig 7, can be built in a similar way—such histograms can be used for region description.

clip_image005

Fig 7: Curvature

o Bending energy

The bending energy (BE) of a border (curve) is the energy necessary to bend the rod to the desired shape, and can be computed as a sum of squares of the border curvature c(k) over the border length L.

image

image

o Signature

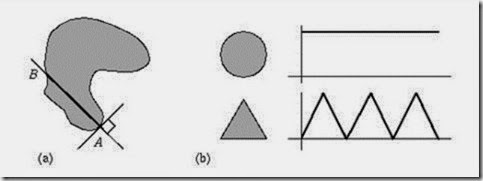
The signature of a region is obtained as a sequence of normal contour distances. The normal contour distance is calculated for each boundary element as a function of the path length. For each border point A, the shortest distance to an opposite border point B is sought in a direction perpendicular to the border tangent at point A (Fig 9). Signatures may be applied to the recognition of overlapping objects or whenever only partial contours are available.

clip_image010

Fig 9: Signature (a) Construction (b) Signatures for a circle and a triangle

o Chord distribution

Chord is a line joining any two points of the region boundary. Distribution of lengths and angles of all chords on a contour may be used for shape description.

Let b(x, y) = 1 represent the contour points, and b(x, y) = 0 represent all other points. The chord distribution can be computed (Fig 10(a)) as

image

Comments

Post a Comment

Popular posts from this blog

Top hat transformation

By -
Image
• The top hat transformation is used as a simple tool for segmenting objects in gray-scale images that differ in brightness from background, even when the background is of uneven gray-scale. • The top hat transform is superseded by the watershed segmentation for more complicated backgrounds. • Assume a gray-level image X and a structuring element K. The residue of opening as compared to original image X ∖ (X ∘ K) constitutes a new useful operation called a Top hat transformation. • The top hat transformation is a good tool for extracting light objects on a dark but slowly changing background. Those parts of the image that cannot fit into structuring element K are removed by opening. • Subtracting the opened image from the original provides an image where removed objects stand out. • The actual segmentation can be performed by simple thresholding (Fig 18). • If an image were a hat, the transformation would extract only the top of it, provided that the structuring element is larger...
Read more

Digital Image Processing part1

By -
Image
SEGMENTATION THRESHOLDING • Segmentation is the process of partitioning a digital image into multiple segments (sets of pixels, also known as super pixels). • The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze. • Image segmentation is typically used to locate objects and boundaries (lines, curves, etc.) in images. • More precisely, image segmentation is the process of assigning a label to every pixel in an image such that pixels with the same label share certain visual characteristics. • Complete segmentation - set of disjoint regions uniquely corresponding with objects in the input image. • Cooperation with higher processing levels which use specific knowledge of the problem domain is necessary. • Partial segmentation - regions do not correspond directly with image objects. • Image is divided into separate regions that are homogeneous with respect to a chosen property such as bright...
Read more

Basics of Spatial Filtering,Frequency Domain filters and Homomorphic filtering

By -
Image
Basics of Spatial Filtering some neighborhood operations work with the valuesof the image pixels in the neighborhood and the corresponding values of asubimage that has the same dimensions as the neighborhood.The subimage iscalled a f i l t e r , m ask , k ernel, template, or window , with the first three terms beingthe most prevalent terminology.The values in a filter subimage are referred toas coefficients , rather than pixels. The concept of filtering has its roots in the use of the Fourier transform for signal processing in the so-called f r equency domain . This topic is discussed in more detail in Chapter 4. In the present chapter, we are interested in filtering operations that are performed directly on the pixels of an image.We use the term spatial filtering to differentiate this type of process from the more traditional frequency domain filtering. The mechanics of spatial filtering are illustrated infig.The process consists simply of moving the filter mask from point to poi...
Read more