Basics of Spatial Filtering,Frequency Domain filters and Homomorphic filtering
Basics of Spatial Filtering
some neighborhood operations work with the valuesof the image pixels in the neighborhood and the corresponding values of asubimage that has the same dimensions as the neighborhood.The subimage iscalled a filter,mask, kernel, template, or window, with the first three terms beingthe most prevalent terminology.The values in a filter subimage are referred toas coefficients, rather than pixels.
The concept of filtering has its roots in the use of the Fourier transform for signal processing in the so-called frequency domain. This topic is discussed in more detail in Chapter 4. In the present chapter, we are interested in filtering operations that are performed directly on the pixels of an image.We use the term spatial filtering to differentiate this type of process from the more traditional frequency domain filtering.
The mechanics of spatial filtering are illustrated infig.The process consists simply of moving the filter mask from point to point in an image. At each point (x, y), the response of the filter at that point is calculated using a predefined relationship. For linear spatial filtering (see Section 2.6 regarding linearity), the response is given by a sum of products of the filter coefficients and the corresponding image pixels in the area spanned by the filter mask.For the 3*3 mask shown in the result (or response), R, of linear filtering with the filter mask at a point (x, y) in the image is which we see is the sum of products of the mask coefficients with the corresponding pixels directly under the mask. Note in particular that the coefficient w(0, 0) coincides with image value f(x, y), indicating that the mask is centered at (x, y) when the computation of the sum of products takes place. For a mask of size m*n, we assume that m=2a+1 and n=2b+1,where a and b are nonnegative integers. All this says is that our focus in the following discussion will be on masks of odd sizes, with the smallest meaningful size being
Smoothing Spatial Filters
Smoothing filters are used for blurring and for noise reduction. Blurring is used in preprocessing steps, such as removal of small details from an image prior to (large) object extraction, and bridging of small gaps in lines or curves. Noise reduction can be accomplished by blurring with a linear filter and also by nonlinear filtering.
Smoothing Linear Filters
The output (response) of a smoothing, linear spatial filter is simply the average of the pixels contained in the neighborhood of the filter mask. These filters
sometimes are called averaging filters. For reasons explained in Chapter 4, they also are referred to a lowpass filters.
The idea behind smoothing filters is straightforward. By replacing the value of every pixel in an image by the average of the gray levels in the neighborhood defined by the filter mask, this process results in an image with reduced “sharp” transitions in gray levels. Because random noise typically consists of sharp transitions in gray levels, the most obvious application of smoothing is noise reduction. However, edges (which almost always are desirable features of an image) also are characterized by sharp transitions in gray levels, so averaging filters have the undesirable side effect that they blur edges. Another application of this type of process includes the smoothing of false contours that result
Sharpening Spatial Filters
The principal objective of sharpening is to highlight fine detail in an image or to enhance detail that has been blurred, either in error or as a natural effect of
a particular method of image acquisition. Uses of image sharpening vary and include applications ranging from electronic printing and medical imaging to industrial inspection and autonomous guidance in military systems.
In the last section, we saw that image blurring could be accomplished in the spatial domain by pixel averaging in a neighborhood. Since averaging is analogous to integration, it is logical to conclude that sharpening could be accomplished by spatial differentiation.This, in fact, is the case, and the discussion in this section deals with various ways of defining and implementing operators for sharpening by digital differentiation. Fundamentally, the strength of the response of a derivative operator is proportional to the degree of discontinuity of the image at the point at which the operator is applied.Thus, image differentiation enhances edges and other discontinuities (such as noise) and deemphasizes areas with slowly varying gray-level values.
In the two sections that follow, we consider in some detail sharpening filters that are based on first- and second-order derivatives, respectively. Before proceeding with that discussion, however, we stop to look at some of the fundamental properties of these derivatives in a digital context. To simplify the explanation, we focus attention on one-dimensional derivatives. In particular, we are interested in the behavior of these derivatives in areas of constant gray level (flat segments), at the onset and end of discontinuities (step and ramp discontinuities), and along gray-level ramps.These types of discontinuities can be used to model noise points, lines, and edges in an image.The behavior of derivatives during transitions into and out of these image features also is of interest.
The derivatives of a digital function are defined
Frequency Domain filters:
The frequency domain methods of image enhancement are based on convolution theorem. This isrepresented as,
The function H (u, v) in equation is called transfer function. It is used to boost the edges of inputimage f (x, y) to emphasize the high frequency components.
The different frequency domain methods for image enhancement are as follows.
1. Contrast stretching.
2. Clipping and thresholding.
3. Digital negative.
4. Intensity level slicing and
5. Bit extraction.
Contrast Stretching:
Due to non-uniform lighting conditions, there may be poor contrast between the background andthe feature of interest. Figure shows the contrast stretching transformations.
These stretching transformations are expressed asIn the area of stretching the slope of transformation is considered to be greater than unity. Theparameters of stretching transformations i.e., a and b can be determined by examining thehistogram of the image. Clipping and Thresholding:
Clipping is considered as the special scenario of contrast stretching. It is the case in which the parameters are α = γ = 0. Clipping is more advantageous for reduction of noise in input signals ofrange [a, b].
Threshold of an image is selected by means of its histogram
Digital Negative:
The digital negative of an image is achieved by reverse scaling of its grey levels to the transformation. They are much essential in displaying of medical images.
Intensity Level Slicing:
The images which consist of grey levels in between intensity at background and other objects require to reduce the intensity of the object. This process of changing intensity level is done withthe help of intensity level slicing. They are expressed as
Homomorphic filtering:
The illumination-reflectance model can be used to develop a frequency domain procedure for improving the appearance of an image by simultaneous gray-level range compression and contrast enhancement. An image f(x, y) can be expressed as the product of illumination andreflectance components:
Equation above cannot be used directly to operate separately on the frequency components of illumination and reflectance because the Fourier transform of the product of two functions is not
separable; in other words,
where Fi (u, v) and Fr (u, v) are the Fourier transforms of ln i(x, y) and ln r(x, y), respectively. If
we process Z (u, v) by means of a filter function H (u, v) then, from
where S (u, v) is the Fourier transform of the result. In the spatial domain
Finally, as z (x, y) was formed by taking the logarithm of the original image f (x, y), the inverse
(exponential) operation yields the desired enhanced image, denoted by g(x, y); that is,




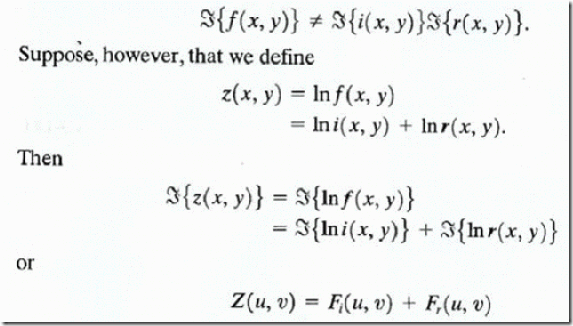
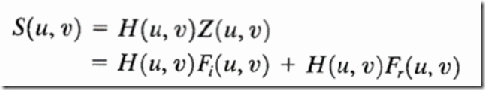


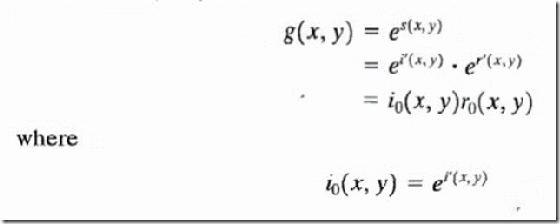




Comments
Post a Comment